Misura della carica elementare con una cella elettrolitica
-
Fisica
-
Classi: 2° biennio
-
-
-
Strumentazione di base
-
Misura o verifica
-
2 h
-
Min. 2 persone
-
Richiede precauzioni
Riassunto / Abstract
Ci si propone di stimare il valore della carica elementare usando una cella elettrolitica. La prova può essere affrontata in una classe IV durante lo studio della conduzione. Si colloca facilmente come competenza interdisciplinare tra le materie di chimica e fisica. Si presta ad utili approfondimenti e/o può essere proposta a conclusione di un percorso chimico-fisico sullo studio della conducibilità nelle soluzioni e dopo aver trattato l'elettrolisi come ad es. in 35-Scienze.
Scheda sintetica delle attività
Realizzare una cella elettrolitica con due laminette di rame e una soluzione di $CuSO_4$ .
Alimentare la cella con corrente costante per un certo tempo. Il rame dell’anodo reagisce con lo ione solfato e passa in soluzione, al catodo lo ione rameico si riduce e si deposita. Al netto la reazione sottrae rame all’anodo e lo deposita al catodo. Dalla variazione di massa, dalle caratteristiche chimiche del rame e dalla misura della corrente che ha attraversato la cella, si determina il numero di cariche elementari scambiate e da qui la carica dell'elettrone: e.
Alimentare la cella con corrente costante per un certo tempo. Il rame dell’anodo reagisce con lo ione solfato e passa in soluzione, al catodo lo ione rameico si riduce e si deposita. Al netto la reazione sottrae rame all’anodo e lo deposita al catodo. Dalla variazione di massa, dalle caratteristiche chimiche del rame e dalla misura della corrente che ha attraversato la cella, si determina il numero di cariche elementari scambiate e da qui la carica dell'elettrone: e.
Si ripete il procedimento in modo da avere più misure di cui si farà la media.
Risorse necessarie
- Soluzione di CuSO4 1M;
- un becher da 250mL;
- due laminette di rame che fungono da elettrodi;
- un amperometro;
- un alimentatore in cc o una pila da 9V;
- 3 cavetti + 2 coccodrilli;
- cronometro;
- bilancia con sensibilità 0,01g;
- carta vetrata, carta da cucina;
- materiale opzionale: due treppiedi, due mezze aste, due morsetti, due pinze.
Prerequisiti necessari
- Saper lavorare con il concetto di mole e di valenza;
- conoscere il comportamento dei sali in soluzione;
- conoscere l’elettrolisi;
- saper realizzare un semplice circuito elettrico;
- saper usare il tester.
Obiettivi di apprendimento
- Verificare le conoscenze teoriche sulla corrente;
- saper confrontare il comportamento di conduttori metallici e soluzioni elettrolitiche;
- saper ricavare informazioni sulle grandezze microscopiche a partire da misure di grandezze macroscopiche.
Dotazioni di sicurezza
- Il solfato di rame è irritante e inquinante, usare i guanti.
- Pericolo di scariche elettriche.
- Vengono usate correnti dell'ordine di 1A; una tale intensità può essere pericolosa, staccare sempre l'alimentazione quando si opera sul circuito.
Svolgimento
Realizzazione delle misure
- Produrre 250 mL di soluzione 1M di $CuSO_4$, seguendo le norme di sicurezza.
- Pulire gli elettrodi grattandoli con carta vetrata in modo da eliminare tracce di ossido. Lavarli con acqua distillata e asciugarli accuratamente.
- Pesare l’elettrodo che funge da anodo (elettrodo positivo) sulla bilancia elettronica.
- Realizzare il circuito secondo lo schema di figura 1.

- Alimentare la cella con corrente costante dell’ordine di 1 A per 2 min o più, prestando attenzione alle norme di sicurezza.
- Estrarre l’anodo, tamponare delicatamente con la carta, aspettare qualche secondo che si asciughi completamente e pesarlo (può essere utile disporre di un asciugacapelli).
- Rimettere l’elettrodo di rame in soluzione e ripetere il procedimento.
Accorgimenti e cause d’errore
- La concentrazione 1M della soluzione non è un valore prescrittivo, tuttavia la soluzione non può essere troppo diluita poiché la corrente risulterebbe troppo bassa allungando i tempi.
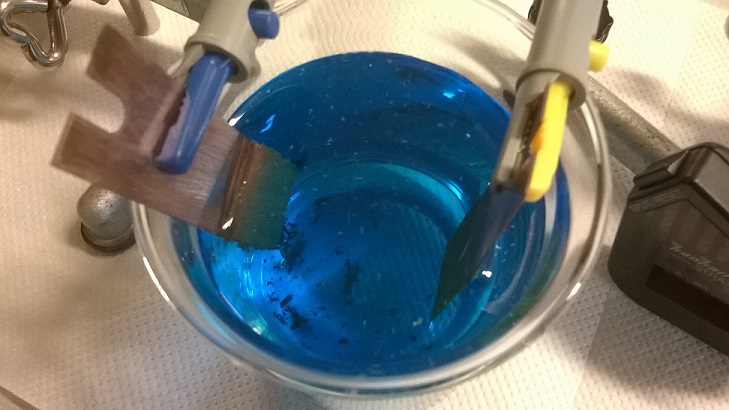
- Pesare sempre l’anodo e non il catodo poiché il deposito di rame non è regolare (figura 2) e precipita nella soluzione rendendo di fatto impossibile la determinazione della massa. Infatti nelle elettrodeposizioni industriali vengono aggiunti dei complessanti alla soluzione per favorire l’adesione all’elettrodo.
- Mantenere costante la corrente, a questo proposito è utile disporre di un alimentatore in cui si possa eventualmente regolare la tensione o usare un reostato. Si può tener conto di eventuali fluttuazioni mediando il valore iniziale e finale, ma di fatto la stabilizzazione della corrente è piuttosto rapida e si può semplicemente trascurare.
- Porre attenzione a che le laminette non si tocchino.
- La maggior causa d’errore è nell’asciugare l’anodo per pesarlo, non va strofinato perchè si potrebbe asportare del rame, ma non deve essere umido per non falsare la misura. Una soluzione potrebbe essere quella di asciugarlo con un asciugacapelli.
- In luogo delle laminette, si possono usare i fili di rame dei fili elettrici. I risultati sono compatibili, occorre però una “treccia” consistente di fili altrimenti occorre usare una tensione più elevata. Attenzione ad usare i fili di rame dei rocchetti spesso in dotazione ai laboratori di fisica. Essi sono verniciati, dunque prima di usarli occorre “grattarli” con carta vetrata.
Elaborazione delle misure
Sia $\Delta m$ la variazione di massa dell'anodo a seguito del passaggio di una corrente di intensità i per un tempo t.
La quantità di carica elettrica che ha attraversato la cella è:
$$Q = i \cdot t$$
$$Q = i \cdot t$$
Il numero di ioni rame ($N_{Cu}$) passati in soluzione dall'anodo è:
$$N_{Cu} = N_A \frac {\Delta m}{M_{Cu}}$$
$$N_{Cu} = N_A \frac {\Delta m}{M_{Cu}}$$
dove: $N_A = 6,022 \cdot 10^{23} [mol^{-1}]$ è il numero di Avogadro;
$M_{Cu} = 63,54\ [g/mol]$ è la massa molare del rame.
Ogni ione rame ($Cu^{2+}$) ha valenza $V_{Cu}=2$, il numero di cariche elementari che ha attraversato la cella è $N_{Cu}\cdot V_{Cu}$, dunque la carica elementare sarà:
$$e = \frac{Q}{N_{Cu} \cdot V_{Cu}}$$
$M_{Cu} = 63,54\ [g/mol]$ è la massa molare del rame.
Ogni ione rame ($Cu^{2+}$) ha valenza $V_{Cu}=2$, il numero di cariche elementari che ha attraversato la cella è $N_{Cu}\cdot V_{Cu}$, dunque la carica elementare sarà:
$$e = \frac{Q}{N_{Cu} \cdot V_{Cu}}$$
Condividere le misure di tutti i gruppi ricavando la media e l'errore, confrontare il valor medio ricavato con il valore atteso e determinarne la variazione percentuale.
E' utile discutere in classe sulle cause d'errore al fine di riconoscere quali variabili lo determinano e quindi dove agire per migliorare l'esperimento.
Si scopre che, pur avendo errori piuttosto grandi, il valore medio di e risulta sempre abbastanza accurato, generalmente scostandosi dal valore atteso entro il 10%.
E' utile discutere in classe sulle cause d'errore al fine di riconoscere quali variabili lo determinano e quindi dove agire per migliorare l'esperimento.
Si scopre che, pur avendo errori piuttosto grandi, il valore medio di e risulta sempre abbastanza accurato, generalmente scostandosi dal valore atteso entro il 10%.
Trattamento e analisi dei dati
L'errore di ogni lettura è assunto sempre pari alla "mezza divisione" ossia a metà della sensibilità dello strumento.
L'errore sulla grandezze derivate si determina come descritto in 6-Fisica ossia in quadratura assumendo variabili indipendenti.
Se ad esempio $\sigma_1$ e $\sigma_2$ sono gli errori assoluti delle grandezze 1 e 2, l'errore assoluto della loro somma o differenza sarà:
$$\sigma = \sqrt{\sigma_1^2 + \sigma_2^2}$$
Analogamente l'errore relativo di un prodotto (o quoziente) sarà la radice quadrata della somma dei quadrati degli errori relativi dei fattori.
Per non appesantire la trattazione metto in allegato il file con lo svolgimento dei passaggi per il calcolo dettagliato degli errori.
L'errore sulla grandezze derivate si determina come descritto in 6-Fisica ossia in quadratura assumendo variabili indipendenti.
Se ad esempio $\sigma_1$ e $\sigma_2$ sono gli errori assoluti delle grandezze 1 e 2, l'errore assoluto della loro somma o differenza sarà:
$$\sigma = \sqrt{\sigma_1^2 + \sigma_2^2}$$
Analogamente l'errore relativo di un prodotto (o quoziente) sarà la radice quadrata della somma dei quadrati degli errori relativi dei fattori.
Per non appesantire la trattazione metto in allegato il file con lo svolgimento dei passaggi per il calcolo dettagliato degli errori.
In allegato anche il foglio di calcolo per l'elaborazione delle misure.
Esempio dati raccolti in aula
- Massa molare del Cu, M= 63,54 g/mol
- Valenza del Cu nel solfato rameico, V = 2
- Massa iniziale anodo = 6,36g
- d.d.p. agli elettrodi = 10V circa
- distanza tra le laminette: 4cm circa
- sensibilità dell'amperometro = 0,01A
- sensibilità del cronometro = 1 s
- sensibilità della bilancia = 0,01 g

L’ultima riga si riferisce ad una prova fatta con la treccia di fili di rame al posto della laminetta, con distanza 2 cm tra gli elettrodi.
Osservando la tabella ci si accorge che gli errori sono decisamente grandi e in massima parte determinati dall'errore sulla massa, la causa è senz'altro nell'aver utilizzato una bilancia con una scarsa sensibilità. Si può migliorare almeno in parte la misura trattando tempi più lunghi in modo che la variazione della massa sia più consistente.
E' comunque interessante notare che anche se abbiamo usato variazioni di massa esigue, l’ordine di grandezza di e è sempre corretto. La media dei valori ottenuti è:
$$ e = \left( 1,65 \pm 0,13 \right) \cdot 10^{-19}\ C$$
mostra un errore relativo dell'8% circa.
Il risultato è piuttosto soddisfacente dal momento che questo valore si discosta solo del 3,4% dal valore atteso $e = 1,6021776 \cdot 10^{-19}\ C$ e risulta quindi con esso compatible, nonostante la strumentazione non particolarmente raffinata utilizzata.
Osservando la tabella ci si accorge che gli errori sono decisamente grandi e in massima parte determinati dall'errore sulla massa, la causa è senz'altro nell'aver utilizzato una bilancia con una scarsa sensibilità. Si può migliorare almeno in parte la misura trattando tempi più lunghi in modo che la variazione della massa sia più consistente.
E' comunque interessante notare che anche se abbiamo usato variazioni di massa esigue, l’ordine di grandezza di e è sempre corretto. La media dei valori ottenuti è:
$$ e = \left( 1,65 \pm 0,13 \right) \cdot 10^{-19}\ C$$
mostra un errore relativo dell'8% circa.
Il risultato è piuttosto soddisfacente dal momento che questo valore si discosta solo del 3,4% dal valore atteso $e = 1,6021776 \cdot 10^{-19}\ C$ e risulta quindi con esso compatible, nonostante la strumentazione non particolarmente raffinata utilizzata.
Note e storia
L’esperimento può essere proposto anche con elettrodi di zinco (che di solito fanno parte della dotazione dei laboratori di Fisica) in soluzione di $Zn^{2+}$ e si ottengono risultati confrontabili con quelli proposti.
Bibliografia
- S.J. Pugliese, Una misurazione elettrolitica della carica di e, La fisica nella scuola, anno XXVIII (1995) pag 185
- Per le modalità d'uso del solfato rameico si veda: http://it.wikipedia.org/wiki/Solfato_rameico
Altre esperienze sulla stima della carica elementare, ma di taglio più chimico si possono trovare in:
Autori
Arvati Susanna

