Gli errori di misura con il metodo Monte Carlo
-
Fisica
-
Classi: 1° biennio e 2° biennio e 5° anno
-
-
-
Laboratorio virtuale
-
Misura o verifica
-
1 h
-
Min. 1 persona
-
Nessuna
Riassunto / Abstract
Il calcolo analitico degli errori per le grandezze derivate può essere complicato e richiede dimestichezza con le derivate (parziali). Il metodo Montecarlo simula l'effetto di una distribuzione statistica e permette di valutare velocemente gli errori in modo empirico.
Scheda sintetica delle attività
Si utilizza un foglio elettronico per generare distribuzioni di valori che simulino ipotetiche misure ripetute. Da queste si può stimare l'incertezza su eventuali grandezze derivate e verificare in modo empirico le leggi di propagazione delle incertezze di misura.
Risorse necessarie
- Foglio elettronico.
Prerequisiti necessari
- Uso di un foglio elettronico;
- nozioni di base sulle incertezze di misura e sul trattamento degli errori.
Obiettivi di apprendimento
- Quantificare l'effetto della propagazione delle incertezze di misura su grandezze derivate;
- verificare in modo empirico le formule per la propagazione delle incertezze di misura;
- utilizzare uno strumento semplice per il calcolo degli errori.
Dotazioni di sicurezza
Nessuna
Svolgimento
Introduzione
Una misura, per quanto precisa e accurata, non fornisce mai un valore esatto, quindi l'incertezza è un fattore intrinseco, non eliminabile, nel processo di misura di qualunque grandezza fisica! Quindi l'incertezza caratterizza la qualità di una misura ed è indispensabile quantificarla, senza questa informazione il risultato ottenuto non può essere confrontato con altri risultati o con valori di riferimento. E' evidente che i criteri che definiscono la qualità di una misura devono essere chiari e condivisi.
Il testo di riferimento per il trattamento degli errori e delle incertezze di misura è la guida GUM (1) (Guide to the Expression of Uncertainty in Measurement) pubblicata dal BIPM (Bureau International des Poids et Mesures). HTML, PDF.
Le raccomandazioni della guida stabiliscono che l'incertezza di una misura sia definita tramite la varianza $\sigma^2$ (stimata tramite un calcolo statistico o valutata in altro modo) della distribuzione dei valori del misurando (GUM - 0.7). L'errore standard su un valore misurato o valutato da misure indirette definito come la deviazione standard σ.
Perché usare la varianza per stimare l'errore?
Ci sono almeno tre motivi per usare la deviazione standard (o la varianza) come parametro per quantificare l'incertezza di misura:
- Il teorema di Cebychev [2] stabilisce un massimo alla probabilità che l'errore di una misura sia maggiore di nσ.
- Il criterio di Chauvenet [3] ci fornisce un metodo per riconoscere ed eventualmente escludere gli outlayer.
- Nel caso di grandezze derivate, misure indirette, la legge per la propagazione degli errori richiede che gli errori siano espressi in termini di deviazione standard (GUM - E.4)
Definizioni
Dato un insieme di N valori della grandezza X, la media è definita come:
$$\bar{x} = \frac{1}{N} \sum_{i=1}^N\left(x_i - \bar{x}\right)^2\ \ \ \ \ \ [1]$$
La varianza campionaria è:
$$s^2 = \frac{1}{N-1}\sum_{i=1}^N \left(x_i - \bar{x} \right)^2\ \ \ \ \ \ \ [2]$$
La deviazione standard campionaria è, ovviamente, s.
$\bar{x}$ e s sono rispettivamente una stima del valore atteso $\mu$ e della deviazione standard $\sigma$ della distribuzione dei valori della grandezza x.
$$\bar{x} = \frac{1}{N} \sum_{i=1}^N\left(x_i - \bar{x}\right)^2\ \ \ \ \ \ [1]$$
La varianza campionaria è:
$$s^2 = \frac{1}{N-1}\sum_{i=1}^N \left(x_i - \bar{x} \right)^2\ \ \ \ \ \ \ [2]$$
La deviazione standard campionaria è, ovviamente, s.
$\bar{x}$ e s sono rispettivamente una stima del valore atteso $\mu$ e della deviazione standard $\sigma$ della distribuzione dei valori della grandezza x.
L'errore standard sulla media (deviazione standard della distribuzione delle medie campionarie) è:
$$\sigma_{\bar{x}} = \frac{s}{\sqrt{N}}\ \ \ \ \ \ \ [3]$$
$$\sigma_{\bar{x}} = \frac{s}{\sqrt{N}}\ \ \ \ \ \ \ [3]$$
Nota: la funzione DEV.ST() dei fogli elettronici (Excel, Calc) calcola la deviazione standard campionaria, per calcolare la deviazione standard (σ) bisogna usare la funzione DEV.ST.POP()
Propagazione degli errori
Se $Y = f\left(X_1, X_2, ...X_k\right)$ è una grandezza derivata, funzione di k grandezze $X_1, X_2,...X_k$ delle quali conosciamo valori ($x_j$) e incertezza ($\sigma_j$), la varianza della distribuzione della Y è data da:
$$\sigma_Y^2 = \sum_{j=1}^k \large{|}\frac{\partial f}{\partial X_j}\large{|}^2 \sigma_j^2\ \ \ \ \ \ \ [4]$$
e l'incertezza su Y è:
$$\sigma_Y = \sqrt{\sigma_Y^2}$$
$$\sigma_Y^2 = \sum_{j=1}^k \large{|}\frac{\partial f}{\partial X_j}\large{|}^2 \sigma_j^2\ \ \ \ \ \ \ [4]$$
e l'incertezza su Y è:
$$\sigma_Y = \sqrt{\sigma_Y^2}$$
Nota: La [4] è valida se le grandezze $X_j$ sono tutte indipendenti tra loro. In caso contrario andrebbe considerato l'effetto della correlazione.
Il metodo Montecarlo
L'applicazione della (4) per la stima degli errori può risultare complicata se la funzione f(X1,X2,...Xk) è complessa e, soprattutto, se i ragazzi non hanno dimestichezza (o non conoscono) le derivate. Possiamo però utilizzare un approccio alternativo per valutare l'errore su una grandezza derivata noto come metodo Montecarlo (3).
Il metodo Montecarlo [4] è una procedura empirica di simulazione che permette di ottenere stime di parametri di un modello (ad esempio per una distribuzione di probabilità) mediante un campionamento casuale dei possibili risultati di un'osservazione. Il metodo consiste nel calcolare una serie di possibili realizzazioni del fenomeno in esame, si utilizza poi la distribuzione dei risultati ottenuti per stimare numericamente indici statistici e caratteristiche quantitative. Questo approccio permette di superare la complessità dei calcoli analitici quando i fenomeni in esame diventano complessi, ad esempio sono utilizzati per le simulazioni della risposta nei rivelatori per esperimenti di alte energie .
Qui lo usiamo per valutare l'errore nel caso di grandezze derivate seguendo lo schema seguente: supponiamo che la grandezza Y sia una funzione f(X1, X2,..., Xk ) di k variabili delle quali abbiamo misurato o comunque conosciamo il valore: x1, x2, ... xk e le rispettive incertezze: σ1, σ2, ..., σk.
- per ognuna delle variabili Xi si costruisce una distribuzione di valori opportuna con valore atteso μi=xi e deviazione standard σi
- Si calcolano possibili valori della Y prendendo casualmente i valori delle variabili dalle distribuzioni: $$Y_h = f\left(x_1^{h}, x_2^{h}, ...x_k^{h} \right)$$
- Il valore medio della distribuzione delle $Y_h$ sarà molto vicino al valore calcolato usando i valori medi: $$\bar{Y}_h = f\left(x_1, x_2, ...x_k \right)$$
- mentre la deviazione standard della distribuzione delle $Y_h$ rappresenta una stima dell'incertezza su $Y$.
Funzioni Excel (Microsoft) o Calc (Open Office)
Il procedimento è implementato nel foglio EXCEL allegato (LINK). Descriviamo qui le funzioni usate nel foglio EXEL. Le stesse funzioni sono disponibili nei fogli elettronici dei pacchetti OpenOffice e LibreOffice e funzioni analoghe si trovano in tutti i programmi più o meno sofisticati di analisi statistica.
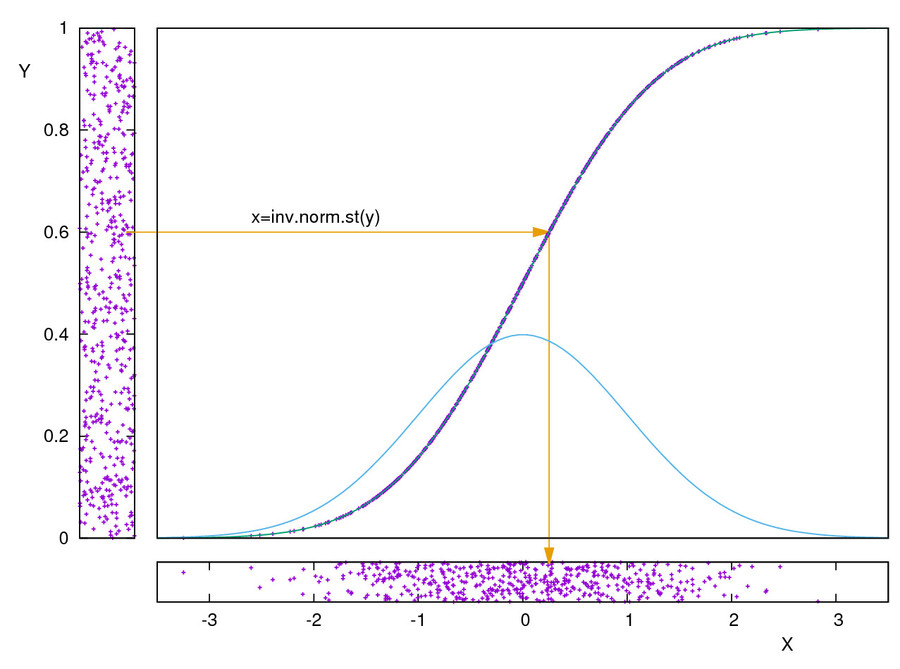
La funzione INV.NORM.ST() è la funzione inversa della distribuzione di densità di probabilità di Gauss standard.
La funzione CASUALE() genera una sequenza di numeri casuali uniformemente distribuiti nell'intervallo [0:1]. La sequenza viene aggiornata aggiornando il foglio oppure premendo il tasto F9 (Excel)
La funzione: INV.NORM.ST(CASUALE()) genera una sequenza di numeri casuali con distribuzione normale standard: ovvero valore atteso nullo (μ=0) e deviazione standard unitaria (σ=1) (vedi figura 1)
La funzione Xo +S*INV.NORM.ST(CASUALE()) genera una sequenza di numeri casuali con distribuzione normale con valore atteso μ=Xo e deviazione standard σ=S.
Con un po' di dimestichezza con i fogli elettronici si possono usare le distribuzioni fornite per
- calcolare l'incertezza su grandezze derivate;
- verificare il teorema del limite centrale (equazione [3])
- verificare empiricamente la validità delle regole di propagazione degli errori per espressioni semplici, ad esempio:
$$ A=B+C \longrightarrow \sigma_A = \sqrt{\sigma_B^2 + \sigma_C^2}$$
$$A = B \cdot C \longrightarrow \sigma_A = A \cdot \sqrt{\left(\frac{\sigma_B}{B}\right)^2 + \left(\frac{\sigma_C}{C}\right)^2}$$
$$A = B \cdot C \longrightarrow \sigma_A = A \cdot \sqrt{\left(\frac{\sigma_B}{B}\right)^2 + \left(\frac{\sigma_C}{C}\right)^2}$$
Il foglio EXCEL (link) contiene alcune cartelle per il calcolo di funzioni semplici (A+B, A-B, A*B, A(1-Bexp(-C))) e può essere modificato a piacere.
Note e storia
Nota storica
Il testo di riferimento per il trattamento degli errori e delle incertezze di misura è la GUM (Guide to the Expression of Uncertainty in Measurement)[1] pubblicata dal BIPM (Bureau International des Poids et Mesures). HTML, PDF
Il concetto di incertezza come un attributo quantificabile è relativamente recente nella storia della Misura. Come descritto nella GUM è nel 1977 che, riconoscendo una generale mancanza di consenso sulla definizione di 'incertezza di misura il Comité International des Poids et Mesures (CIPM), richiese al Bureau International des Poids et Mesures (BIPM) di occuparsi del problema e indicare, insieme con i laboratori che si occupano di definire gli "standard" di misura, le raccomandazioni da seguire.
Le prime "indicazioni" risalgono agli anni 80 ma la pubblicazione ufficiale della GUM guida è del 1995. L'ultima versione, com piccole modifiche e precisazioni rispetto alla versione del 95, è del 2009. Non è sorprendente che molti testi di Fisica (al liceo e all'università) pur riconoscendo il ruolo fondamentale dell'incertezza di misura (è spesso il primo argomento trattato) usino definizioni approssimate, non corrette se non sbagliate.
Note:
La diseguaglianza di Cebychev, valida qualunque sia la distribuzione presa in esame (quindi non solo una distribuzione di Gauss), stabilisce che se x è un valore appartenente ad una distribuzione con valore atteso μ e deviazione standard σ, la probabilità che x differisca dal valore vero più di n volte σ è certamente minore di $\large{\frac{1}{n^2}}$:
$$P\left(|x-\mu|> n\sigma\right) \le \frac{1}{n^2}$$
$$P\left(|x-\mu|> n\sigma\right) \le \frac{1}{n^2}$$
Questa diseguaglianza è molto conservativa; ad esempio nel caso di una gaussiana sappiamo che la probabilità che x differisca dal valore vero più di σ è circa il 30% mentre la (1) da un'informazione banale:
$$P\left(|x-\mu|> sigma\right) \le 1$$
$$P\left(|x-\mu|> sigma\right) \le 1$$
Stima della deviazione Standard. Il paragrafo GUM-E.4 stabilisce che, qualora non sia possibile valutare statisticamente la deviazione standard di una misura (es. misure ripetute), sia lecito stimare la varianza anche in base alla "propria esperienza" (Stima di tipo B). Per questo fa notare come l'incertezza relativa sulla stima della deviazione standard sia:
$$\frac{\sigma_s}{s} \simeq \frac{1}{\sqrt{2\left(n-1\right)}}$$
$$\frac{\sigma_s}{s} \simeq \frac{1}{\sqrt{2\left(n-1\right)}}$$
che su 10 misure è circa 24 %.
Bibliografia
Autori
Meneghini Carlo

