Il volto mutevole della Luna: un semplice algoritmo per conoscere le fasi lunari
-
Scienze della Terra
-
Classi: 1° biennio
-
-
-
Laboratorio "povero"
-
Esperimento
-
1 h
-
Min. 1 persona
-
Nessuna
Riassunto / Abstract
I libri di testo e di divulgazione presentano con ampi dettagli il fenomeno delle fasi lunari, la cui ripetizione, ogni 29,53 giorni, è alla base dei primi calendari realizzati dalle diverse culture e civiltà storiche. La comprensione geometrica del fenomeno astronomico è presentata attraverso schemi di semplice ed efficace intuizione.
La proposta di questa esperienza di laboratorio fa riferimento alla meno semplice conoscenza della fase lunare in un dato giorno, in assenza di almanacchi, agende celesti, pubblicazioni dedicate, o programmi-planetario per computer, e utilizza un antico algoritmo, la cui efficacia è stata alla base di una sua ampia diffusione presso le culture contadine europee, almeno dal medioevo ad oggi.
Scheda sintetica delle attività
Attraverso questa esperienza, è possibile calcolare le fasi lunare, osservare le forme della Luna e prevedere alcuni fenomeni naturali. In particolare:
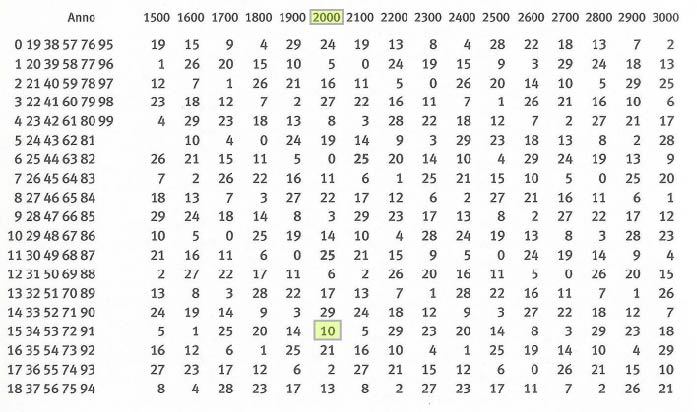
- L'esecuzione dell'algoritmo avviene con l'uso della tabella delle Epatte (tabella1), ed è possibile calcolare la fase lunare per qualsiasi data passata o futura.
- L'identificazione della fase (allegato 1), permette, con l’aiuto della carta morfologica (allegato 2), il riconoscimento delle forme superficiali osservabili.
- La carta geologica dell'emisfero visibile (allegato 3), con le formazioni geologiche di maggior rilievo, consente di individuare le età delle diverse morfologie della superficie lunare (mari, rilievi, grandi crateri da impatto).
- Il calcolo della fase lunare può essere utilizzato anche per la previsione di massima delle maree, tenendo conto della modestia del fenomeno nel Mar Mediterraneo.
- Sono possibili, inoltre, connessioni culturali interdisciplinari con le tradizioni popolari locali, nel merito delle pratiche agricole, dei calendari naturali, di storie e leggende popolari.
Risorse necessarie
- binocolo (di qualsiasi diametro) con stativo (consigliato, ma non indispensabile);
- tabella della epatta (tabella 1).
Prerequisiti necessari
Saper leggere carte geomorfologiche e geologiche.
Obiettivi di apprendimento
- Conoscere in dettaglio il fenomeno delle fasi lunari;
- comprendere i primi calendari, le anomalie delle orbite planetarie, la descrizione e previsione del fenomeno delle maree;
- raggiungere una buona conoscenza della morfologia dell'emisfero visibile del satellite;
- cominciare a riconoscere le principali formazioni geologiche lunari.
Dotazioni di sicurezza
Nessuna
Svolgimento
L'esperienza si basa sul fenomeno delle fasi lunari, la cui ripetizione è fissata dal periodo del mese sinodico di 29,532 gg. Utilizza il ciclo di Metone di 19 anni e il canone di L. Lilio per il calcolo delle epatte (dal greco ηπακτάι ἡμέραι, giorni aggiunti). Tiene conto, con un fattore correttivo, del reale periodo dell'anno tropico, inferiore di circa 11' all'anno giuliano di 365 gg 6 h. La precisione di tale algoritmo è alle 12 ore, e prevede esclusivamente la conoscenza del mese e del giorno per cui si ricerca la fase, oltre alla disponibilità di una tabella (tabella 1) da cui si ricava un numero E, l'epatta, valido per l'intero anno solare che si considera.
Calcolo dell’Epatta
E' possibile, in ogni caso, il calcolo di E con la seguente formula:
$$\textbf {E}= [(b+1) \cdot 11]-c$$
dove:
b, chiamato numero d'oro, è il resto della divisione anno/19 (variabile da 0 a 19);
c vale 12 per il periodo 1799-2199.
Se il risultato è E<0, al valore ottenuto si somma 30; se risulta E> 30, si sottrae 30.
Per l'anno 2014, il numero d’oro è 0 (2014:19=106, con resto 0). Quindi l’epatta è: $$\textbf {E} = [(0+1) \cdot 11]-12= -1$$ Poiché risulta E<0, si aggiunge 30, per cui E=29.
$$\textbf {E}= [(b+1) \cdot 11]-c$$
dove:
b, chiamato numero d'oro, è il resto della divisione anno/19 (variabile da 0 a 19);
c vale 12 per il periodo 1799-2199.
Se il risultato è E<0, al valore ottenuto si somma 30; se risulta E> 30, si sottrae 30.
Per l'anno 2014, il numero d’oro è 0 (2014:19=106, con resto 0). Quindi l’epatta è: $$\textbf {E} = [(0+1) \cdot 11]-12= -1$$ Poiché risulta E<0, si aggiunge 30, per cui E=29.
Calcolo delle fasi lunari
L'algoritmo per il calcolo delle fasi lunari è costituito dalla somma di tre termini:
A (numero annuo dell'Epatta) + B (numero del mese) + C (numero del giorno)
La numerazione del mese non parte da gennaio, ma da marzo (quindi l'epatta dell'anno in corso si applica dal mese di marzo al febbraio successivo, p.e.: epatta 2014=29, vale per il periodo 1 marzo 2014-28 febbraio 2015) .
Calcoliamo, per esempio, la fase lunare di sabato 25 ottobre 2014:
- numero del mese di ottobre (iniziando con marzo): 8;
- numero del giorno: 25;
- numero dell’epatta per il 2014: 29.
La fase lunare del giorno è: 8+25+29 = 62; se il risultato supera 30, si sottrae 30 o un multiplo di 30, per cui in questo caso sarà: $ 62- (30 \cdot 2) = 2$.
La fase del mese sinodico alla data per cui si è effettuato il calcolo indica, quindi, che siamo al 2° giorno. Con l’aiuto di una serie di immagini delle fasi lunari (allegato 1) si può verificare che, in tale condizione, è visibile un’esile falce di luna, con la “gobba a ponente”: risulta pertanto osservabile a occhio nudo il bordo orientale del satellite naturale, basso sull'orizzonte ovest al tramonto.
Note e storia
Note storiche
La conoscenza delle fasi lunari assume un ruolo preminente nelle comunità agricole, per le connessioni con alcuni tipi di coltivazioni, suggerite nella persistente diffusione di pubblicazioni popolari, come “Il calendario di Frate Indovino”, che si basano in larga misura su tradizioni popolari del mondo agricolo, che risalgono agli antichi parapegmi, specie di calendari che raccoglievano informazioni astronomiche, come sorgere tramontare degli astri, e meteorologiche, insieme a notizie astrologiche basate su superstizioni e credenze popolari.
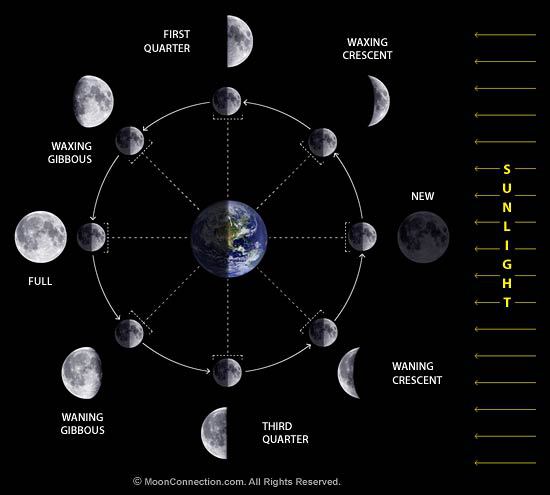
La comprensione geometrica del fenomeno astronomico è presentata attraverso schemi di semplice ed efficace intuizione (figura 1).
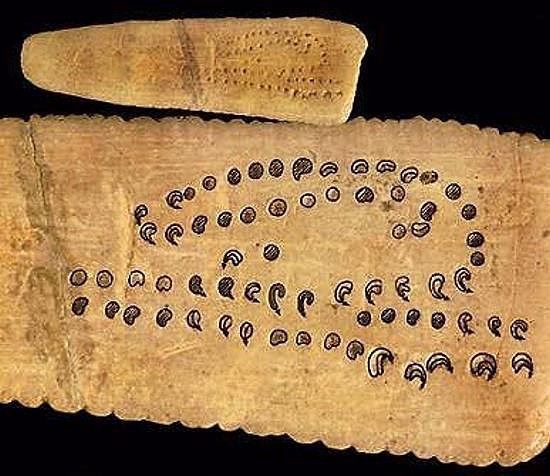
Le prime osservazioni “celesti” dell'Umanità furono sicuramente rivolte al nostro satellite naturale. Le testimonianze paletnografiche di manufatti su materiali vari, con serie di incisioni, rinvenute in siti preistorici, dalla Siberia centrale alla regione dei Laghi in East Africa (Paleolitico Superiore-Neolitico: 40000-6000 anni fa), confermano in modo esplicito l'interesse per l'osservazione della Luna e delle sue fasi per scopi calendariali (figura 2).
Alcune Veneri della cosiddetta Art Mobilier, con serie di 28 incisioni, sono possibilmente collegate a previsioni dei cicli di fertilità (figura 3).

La presenza di manufatti con incisioni in diversi gruppi di 28-29 (figura 4), attesta l'utilizzazione per scopi calendariali e anche di calcolo, forse legati alla previsione dei periodi delle attività di caccia e raccolta.

I reperti recuperati e le testimonianze dei complessi megalitici preistorici dimostrano che esiste una sequenza cronologica nelle prime osservazioni astronomiche, attraverso le diverse culture, che si può schematicamente riassumere: Luna-Sole-stelle. Anche la realizzazione dei calendari ha seguito una genesi simile: i primi calendari storici realizzati in Mesopotamia sono stati esclusivamente lunisolari. La difficoltà a realizzare un soddisfacente calendario, che unisca e mantenga la correlazione fra i tre elementi fondamentali nel computo del tempo: giorno, mese, anno, è conseguenza dei periodi dei tre fenomeni celesti alla base della misura del tempo: durata del giorno solare, mese sinodico della Luna, anno tropico. Questi periodi non sono tra loro commensurabili, ovvero nessuno è reciprocamente un multiplo o sottomultiplo intero. Un mese sinodico, o delle fasi, mediamente misura 29 gg 12 h 44 m; in un anno solare di 365 gg 5 h 49 m 11 s, ci sono 12 mesi sinodici, che assommano a 354 g: rimangono quindi 11 gg e quasi 6 ore di resto. Una prima soluzione al problema di correlare i mesi con l'anno fu di introdurre un anno “intercalare” ogni tre, con 13 mesi lunari. Ma il computo era ancora insufficiente.
Una soluzione soddisfacente per realizzare un calendario lunisolare efficace fu scoperta dall'astronomo ateniese Metone, nel V sec. A.C., che scoprì che 19 anni solari sono pari, quasi esattamente, a 235 mesi sinodici, ovvero 6939,6 gg. Il ciclo di Metone è tutt'oggi utilizzato per la previsione delle fasi lunari, in quanto nel ciclo le fasi lunari si ripetono esattamente nello stesso mese e nello stesso giorno ogni 19 anni. Due riforme calendariali, quella Giuliana del 46 a.C. e la Gregoriana del 1582 d.C., sono state necessarie per introdurre un calcolo del tempo civile efficace, in grado di vincolare l'anno solare con l'inizio astronomico delle stagioni. La previsione delle fasi lunari era comunque di notevole importanza per la Chiesa, ai fini della determinazione delle feste mobili, di cui la principale è la Pasqua, stabilita come prima domenica successiva al primo plenilunio seguente l'equinozio di primavera. Tale calcolo, più complesso che nel calendario giuliano, è stato codificato dal medico e astronomo Luigi Lilio (1510-1574), vero artefice della riforma (figura 5).

La previsione dell'orbita del nostro satellite naturale è stata oggetto di lunghe ricerche. L'orbita della Luna attorno al comune baricentro con la Terra, collocato all'interno del mantello terrestre, a circa 2200 km di profondità, presenta numerosi fattori di perturbazione, che hanno reso un serio problema il calcolo di precisione della posizione del satellite naturale. Una prima descrizione delle anomalie del moto lunare era stata realizzata dall'astronomo greco Hipparcos nel II sec A.C. ed è nota come “Prima anomalia lunare”. Solamente alla fine del XIX secolo l'astronomo canadese-americano Simon Newcomb (1835-1912), formulò una teoria soddisfacente per una precisione adeguata della posizione lunare, che tiene conto di 253 fattori perturbativi principali.
Bibliografia
- La Luna, A. Fresa, ed. Ulrico Hoepli, 1932;
- Il calendario e l'orologio, P. Tempesti, ed. Gremese, 2006;
- Lunario, A. Cattabiani, Oscar Saggi, ed. Mondadori, 2001;
- Planetario, A. Cattabiani, Oscar Saggi, ed. Mondadori, 2001.
Autori
Chirri Maurizio
Lombardi Livia
Lombardi Livia
Schede / Allegati
- Allegato 1 Quadro sinottico fasi lunari
- Allegato 2_Carta morfologica della superficie lunare
- Allegato 3 Carta geologica della Luna

