• Foglio da disegno 50 x 33 circa;
• una matita nuova appuntita di circa 7 cm;
• una matita per disegnare, gomma per cancellare;
• compasso, riga, pennarello indelebile;
• bussola;
• colla o plastilina o gomma da masticare.

• Conoscere il concetto di meridiano, parallelo, reticolo geografico;
• conoscere la differenza tra polo magnetico e polo geografico;
• conoscere i principali moti terrestri e le loro implicazioni.

• Imparare a determinare i punti cardinali di un luogo;
• verificare che il polo geografico e quello magnetico non coincidono e calcolare con approssimazione la declinazione magnetica;
• verificare che il mezzogiorno vero del luogo differisce da quello civile;
• costruire, se possibile, una linea diurna per verificare la variazione dell'altezza del sole durante il giorno e in  giorni diversi dell'anno.

Parte A

1. Ogni gruppo di 4 studenti prepara un foglio da disegno sul quale verranno disegnate circonferenze concentriche, partendo dalla prima di raggio  2 cm e aumentando il raggio delle successive circonferenze di 2 cm, fino al massimo consentito.

                                                                       

              

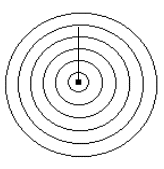
1. In una giornata soleggiata disporre i fogli, perfettamente allineati e leggermente distanziati, sul pavimento di uno spazio, soleggiato almeno fino alle prime ore del pomeriggio, interno o esterno della scuola. Fissare i fogli al pavimento, per evitare spostamenti, con nastro adesivo(spazi interni) o con sassi (se all'esterno)
2. Fissare, con colla o plastilina o con ciò che si ritenga opportuno allo scopo, esattamente al centro delle circonferenze, uno gnomone, rappresentato dalla matita nuova e appuntita.
3. A partire dal mattino, si segna il punto sulla circonferenza dove cade l'ombra della punta dello gnomone. Si ripete l'operazione ogni ora del mattino, comprese le ore 12 registrando accanto al punto l'ora di lettura.

                                                                     

                            

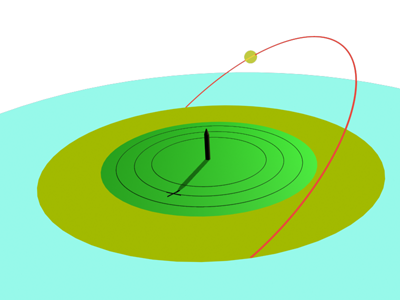
1. Si ripete l'operazione nel pomeriggio, se non e` possibile per tutto il pomeriggio almeno per le prime due ore (fino alle 14). Per evitare disagi durante lo svolgimento delle lezioni mattutine gli incaricati di ogni gruppo effettuerranno la registrazione al cambio di ogni ora.

                                                                   

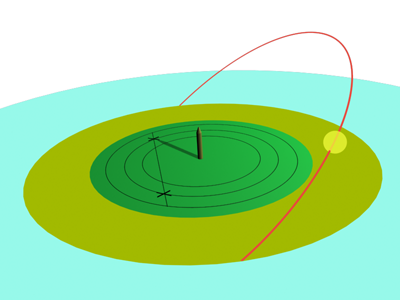
1. A fine giornata o la mattina successiva si individuano due punti, uno del mattino e uno del pomeriggio, che cadano sulla stessa circonferenza e si uniscono con un segmento, si trova esattamente il punto medio del segmento. Con una retta si unisce il punto medio del segmento col centro delle circonferenze: la retta trovata sarà la linea di meridiana del luogo

                                                                     

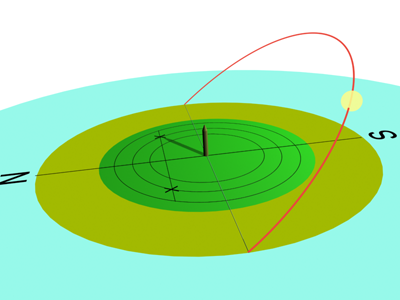
Parte B

1. Si potrà valutare la precisione di ogni gruppo poiché le linee di meridiana di ogni foglio dovrebbero congiungersi perfettamente
2. Si potrà tracciare la linea di meridiana sul pavimento col pennarello indelebile, in modo da poter essere utilizzata durante altre esperienze.
3. Si noterà che la linea di meridiana passerà prossima al punto delle ore 12 senza tuttavia intersecarlo perché il sole culmina sul meridiano del luogo in un tempo diverso dal mezzogiorno civile, a meno che non ci si trovi sul meridiano dell'Etna.
4. Si potrà eventualmente determinare il momento esatto della culminazione del sole sul meridiano osservando quando l'ombra dello gnomone cade esattamente sulla linea meridiana, e calcolare la differenza con l'ora civile
5. Togliendo ora la matita dal centro e ponendo al suo posto una bussola, si fa combaciare il bordo della riga alla direttrice Nord-Sud della bussola. Tenendo salda la riga si fa scorrere la matita, tenuta perpendicolarmente, lungo il suo margine in modo da disegnare la direttrice della bussola sul foglio. Si osserverà che la direttrice della bussola devia di un certo angolo, rispetto alla linea di meridiana. L'angolo, misurabile con un goniometro, determina la declinazione magnetica.
6. Se si uniscono i punti simmetrici registrati durante il giorno sulle circonferenze rispetto alla linea di meridiana, si otterrà una linea curva: un ramo di iperbole che rappresenta la linea diurna. La  linea diurna rappresenta un semplice orologio solare.

                                                                               

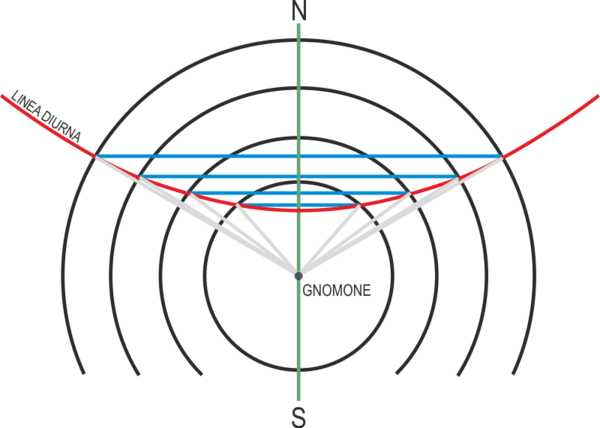
1. Se si disegna la linea diurna durante gli equinozi si osserverà che invece di un'iperbole si ottiene una linea retta.