Misura della componente orizzontale del Campo Magnetico Terrestre

Questa attività si propone di utilizzare il campo magnetico generato da un filo rettilineo percorso da corrente per misurare la componente orizzontale del campo magnetico terrestre, sfruttando la deflessione indotta dal campo magnetico risultante sull'ago di una bussola.

Nessuna

1. Si orienta l'ago magnetico in direzione Nord-Sud. Si posiziona il filo conduttore a una certa distanza d al di sopra dell'ago magnetico, orientandolo nella stessa direzione Nord-Sud; avremo così che il campo magnetico generato dalla corrente che scorre nel filo sarà perpendicolare alla direzione Nord-Sud (figura 1).

                                                                 

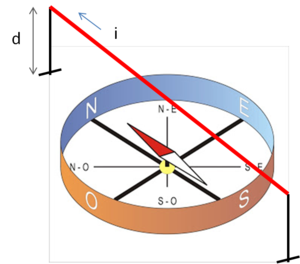
2. Si collega un filo conduttore a un generatore a basso voltaggio e a un tester in serie. Per evitare che i dispositivi di protezione del generatore possano interrompere l'alimentazione per corto circuito, può essere utile aggiungere in serie una resistenza di potenza. Per esempio, per una tensione V = 6V e una corrente i = 4A, sarà necessario inserire una resistenza R = 1.5 Ohm e dissipare una potenza P = 24W                                                 

                                 

 

3. Si misura la distanza tra il filo e la base su cui è posto l'ago magnetico attraverso un righello

4. Si attiva il circuito, aumentando gradualmente l'intensità di corrente nel filo conduttore (per esempio da 0A a 5A) mantenendo costante la distanza tra il filo e l'ago magnetico. All'aumentare della corrente nel circuito, l'ago magnetico ruoterà di un angolo via via maggiore. Per ogni valore della corrente si registra il corrispondente valore dell'angolo $\alpha$ di deflessione dell'ago magnetico, attraverso l'uso di un goniometro.

                                             

 

5. L'intensità del campo magnetico generato dal filo è dato dalla legge di Biot-Savart (unità di misura SI):
$$\left|\vec{B}_i\right| = \frac{\mu_0}{2\pi}\frac{i}{d}\ \ \ \ \ \ \ [1]$$
dove $\mu_0$ è la permeabilità magnetica del vuoto. 
Nella posizione di equilibrio l'ago magnetico si dispone parallelamente al campo magnetico totale, dato dalla somma del campo magnetico terreste $\vec{B}_{terr}$ e del campo magnetico del filo $\vec{B_i}$. In queste condizioni la componente complessiva del campo magnetico perpendicolare all'ago sarà nulla, e quindi le componenti dei due campi magnetici perpendicolari all'ago sono uguali e opposte:
$$ \left| \vec{B}_{terr}\right| \cdot sen\ \alpha =  \left| \vec{B}_{i}\right| \cdot cos\ \alpha \rightarrow$$
$$ \left| \vec{B}_{i}\right|  =  \left| \vec{B}_{terr}\right| \cdot tan\ \alpha\ \ \ \ \ \ \ \ [2]$$

                                                       

6. Combinando le due equazioni [1] e [2] si ottiene:
$$i = \frac{d}{k} \cdot |\vec{B}_{terr}| \cdot tan \alpha$$
con
$$  k = \frac{\mu_0}{2 \pi}$$

Graficando i valori della corrente sull'asse delle ordinate e i valori della tangente dell'angolo di deflessione sull'asse delle ascisse, si ottiene una retta con coefficiente angolare pari a :
$$m = \frac{d}{k} \cdot |\vec{B}_{terr}|$$
Il coefficiente angolare può essere calcolato o graficamente dal rapporto $\large{\frac{\Delta y}{\Delta x}}$ o utilizzando un foglio elettronico (es. EXCEL MS; CALC Oo): le funzioni per trovare le linea di tendenza (o regressione lineare) consentono di calcolare i parametri della retta che meglio approssima i punti del grafico. Si ottengono cosi pendenza (m) e termine noto (intersezione con l'asse delle ordinate). Noto il coefficiente angolare si può così calcolare l'intensità della componente orizzontale del campo magnetico terrestre.
Esempi di dati e di analisi sono riportati nelle relazioni allegate.

7. Si può ripetere questa stessa procedura mantenendo costante la corrente elettrica nel filo e variando la distanza tra la base su cui è posto l'ago magnetico e il filo conduttore.

Campo magnetico terrestre 

La Terra è sede di un campo magnetico la cui origine, e soprattutto il cui mantenimento, è dovuta alla dinamica del ferro fluido presente nel nucleo esterno del pianeta. Il campo magnetico terrestre non si espande liberamente nello spazio interplanetario ma è confinato dal vento solare entro una precisa regione di spazio che prende il nome di magnetosfera terrestre. Conseguenza dell’interazione tra il vento solare e la magnetosfera è la formazione di un complesso sistema di correnti magnetosferiche responsabili della generazione di campi magnetici secondari.  Il campo magnetico misurato sulla superficie del nostro pianeta è pertanto la sovrapposizione di campi di origine interna alla Terra, come quelli prodotti nel nucleo e nella crosta terrestre, e campi di origine esterna, come quelli dovuti alle correnti elettriche che circolano nella ionosfera e nella magnetosfera ed è rappresentato da un campo vettoriale, funzione del punto di osservazione e del tempo, generalmente indicato con F. Introducendo una terna cartesiana levogira con origine nel luogo di osservazione e assi orientati come in figura, si definiscono i seguenti elementi magnetici:

                                                                   

 X componente del vettore nel piano orizzontale, diretta verso il Nord geografico
 Y componente del vettore nel piano orizzontale, diretta verso l’Est geografico
 Z componente verticale, positiva se è diretta verso l’interno della Terra
 H componente orizzontale totale
 F intensità totale del campo
 D declinazione magnetica
 I inclinazione magnetica

Nel S.I. l’unità di misura del campo magnetico terrestre è il Tesla (T), ma nella pratica viene usato un suo sottomultiplo, il nanoTesla pari ad un miliardesimo di Tesla. Sulla superficie terrestre il valore del campo varia in intensità, mediamente da circa 20000 nT all'equatore, a circa 70000 nT ai poli. 

Sul seguente sito è possibile calcolare le diverse componenti del campo magnetico terrestre alla superficie, inserendo la latitudine e la longitudine in gradi decimali o in gradi, minuti, secondi d’arco separati da uno spazio (senza notazioni particolari) , l’elevazione in chilometri, metri o piedi e l’intervallo di tempo:

Bussino Severino
Proietti Orietta
James Irina