Riassunto / Abstract

In questa esperienza una sferetta rotola lungo una rampa arbitrariamente sagomata e poi cade dalla fine della rampa sul pavimento seguendo un moto parabolico con velocità iniziale orizzontale come nell'esperienza 25-Fisica. A differenza di quanto osservato in 25-Fisica in cui si è verificata la conservazione dell'energia meccanica nel moto di rotolamento, qui ci si propone di:

utilizzare la gittata del moto parabolico della sfera come "indicatore" dell'energia persa dalla sfera durante il moto lungo la rampa;
verificare che l'energia meccanica della sferetta non si conserva durante l'esperimento;
valutare la dipendenza dell'energia dissipata dalle caratteristiche della sfera o della superficie della rampa;
quantificare l'energia dissipata in attrito.

Scheda sintetica delle attività

Preparazione di una o più rampe
sistemazione corretta della rampa e misura delle altezze $h_1$ (altezza iniziale della sferetta rispetto al tavolo) e $h_2$ (altezza del tavolo rispetto al pavimento);
misura delle caratteristiche della sferetta (diametro e massa);
esecuzione della prova: misura della gittata e completamente della tabella di raccolta dei dati grezzi;
elaborazione dei dati: calcolo del lavoro dissipato dalle forze di attrito;
considerazioni su come varia il lavoro dissipato al variare del tipo di superficie della rampa (a parità di altezza della rampa $h_1$) e delle caratteristiche della sferetta utilizzata (diametro e massa).

Risorse necessarie

Metro;
calibro;
bilancia elettronica;
cartone (rigido) o compensato;
sferette di diverse dimensioni e/o diverse masse;
carta carbone o sabbia;
tavolo;
filo a piombo;
straccio da cucina e/o tessuto simile a quello degli asciugamani.

Prerequisiti necessari

Lavoro di una forza conservativa e non;
energia cinetica e potenziale;
attrito volvente, attrito del mezzo;
moto di rotolamento, momento d'inerzia;
conservazione dell'energia nel moto di rotolamento;
moto parabolico;
saper utilizzare il calibro;
saper costruire una rampa con del cartone (o compensato).

Obiettivi di apprendimento

Approfondire il moto di rotolamento;
stimare l'energia persa a causa dell'attrito sia volvente che viscoso;
utilizzare la gittata come "misura" della velocità iniziale (orizzontale) di un oggetto;
saper allestire un esperimento con materiale "povero";
saper identificare le cause della perdita di energia meccanica;
saper trarre conclusioni in base ai risultati ottenuti dall'elaborazione dei dati grezzi;
saper identificare e ridurre al minimo le fonti errore nella misura.

Dotazioni di sicurezza

Nessuna

Svolgimento

Costruzione della rampa

La rampa può essere facilmente costruita ritagliando due sagome identiche di cartone (per esempi preso da degli scatoloni): incollando tra di esse un ulteriore strato di cartone più o meno spesso si può cambiare la distanza tra le due guide in modo da ottimizzarla in base al diametro della sfera che si utilizza. Si è verificato che il cartone per imballaggi, pur essendo facilmente ritagliabile del compensato, può causare un attrito volvente no ntrascurabile. Per questo una volta realizzata la rampa è meglio che la superficie di contatto con la sfera sia ricoperta da del cartoncino rigido in modo che il punto di contatto tra la sfera e la rampa sia uno solo. Bisogna fare molta attenzione a che la rampa abbia tangente orizzontale dove termina sul tavolo: per migliorare questa caratteristica conviene far percorre alla sfera una breve distanza sul tavolo stesso (supponendo che esso sia orizzontale). Sarebbe istruttivo costruire almeno un paio di rampe che differiscano non tanto per la forma (che comunque deve assicurare il moto di rotolamento e quindi le pendenze non devono essere troppo elevate) quanto piuttosto per lunghezza totale che la sferetta deve percorrere dal momento del rilascio al momento del distacco dal tavolo in quanto questa lunghezza influenza il lavoro delle forze dissipative durante il rotolamento sulla rampa (l'altezza dell'inizio della rampa può essere mantenuta costante se si vogliono diminuire le misure da effettuare). Con una rampa di forma fissata saranno utilizzate almeno due superifici di contatto: una rigida (tipicamente cartoncino o plastica) ed una molto più deformabile anelasticamente come quella di un panno da cucina che assorbe una discreta quantità di energia.

Dinamica dell'esperimento.

La sfera si trova inizialmente ad altezza $h_1$ rispetto al tavolo e viene lasciata rotolare giù dalla rampa con velocità iniziale nulla. Come osservato in precedenza, conviene lasciar percorrere alla sfera un breve tratto di tavolo (che si assume orizzontale) in modo da essere certi che la sfera lasci il bordo del tavolo con velocità orizzontale di modulo $v$. Se il piano del tavolo si trova ad altezza $h_2$ rispetto al pavimento, la sfera percorre un arco di parabola nel tempo di caduta dall'altezza $h_2$: la proiezione di quest'arco sul pavimento è la gittata $x$.

Misure da effettuare prima di lasciar cadere la sferetta.
E' necessario conoscere dapprima le caratteristiche della sfera utilizzata, ossia il diametro (più facile da misurare del raggio) e la massa. Per la misura del diametro è meglio utilizzare un calibro, per la misura della massa una qualsiasi bilancia elettronica. L'altezza $h_1$ della rampa rispetto al piano del tavolo è facilmente misurabile con un metro, mentre la misura più difficile è la gittata. L'alternativa più semplice è l'utilizzo della carta carbone su un foglio bianco disteso sul pavimento: quando la sfera impatta sulla carta carbone lascia una traccia puntuale della gittata. Si osservi che per misurare al meglio la gittata è opportuno mettere un filo a piombo dal bordo del tavolo al pavimento in modo da identificare chiaramente il punto di inizio della misura per la gittata, come riportato nella figura sottostante. Se la carta carbone non è reperibile, si può utilizzare un sottile strato di sabbia ben spianato e disteso sul pavimento nella zona di caduta (in questo caso l'altezza $h_2$ va misurata con attenzione tenendo conto dello spessore dello strato di sabbia).

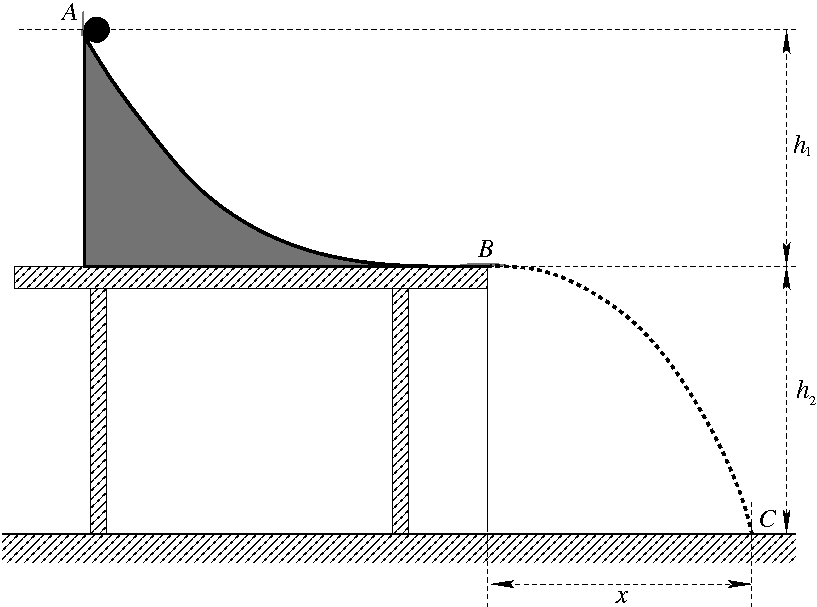
Equazioni di governo in assenza di attrito.
Con riferimento alla figura soprastante, la conservazione dell'energia meccanica (in assenza di attrito), tra il momento della partenza della sfera da ferma (punto A) ed il momento in cui lascia il bordo del tavolo (punto B) con velocità orizzontale del baricentro $v$, assicura che:
$$mgh_1 = \frac{1}{2}mv^2 + \frac{1}{2}I \omega^2$$
dove il momento d'inerzia è calcolato rispetto al baricentro della sfera e vale:
$$I = \frac{2}{5}mR^2$$, essendo $R$ il raggio della sfera.
Siccome nel moto di rotolamento il punto di contato è fermo, la velocità del baricentro della sfera è legata alla velocità angolare dalla relazione $v = \omega R$, pertanto l'energia cinetica di rotazione diventa:
$$\frac{1}{2}I \omega^2 = \frac{1}{2} \cdot \frac{2}{5} mR^2 \cdot \left(\frac{v}{R} \right)^2 = \frac{1}{5}mv^2$$
La conservazione dell'energia meccanica si riduce quindi a:
$$mgh_1 = \frac{1}{2} mv^2 + \frac{1}{2}I \omega^2 \Longrightarrow mgh_1 = \frac{1}{2}mv^2 + \frac{1}{5}mv^2 = \frac{7}{10} mv^2$$
da cui si ricava il valore della velocità del baricentro al momento d'inizio del moto parabolico in aria:
$$v= \sqrt{\frac{10}{7}gh_1}$$

Si osservi che se la sfera non rotolasse ma "scivolasse" lungo la rampa senza trasformare parte dell'energia iniziale in energia di rotazione, si avrebbe: $v = \sqrt{2gh_1}$.
Il tempo di caduta durante il moto parabolico determina la distanza che la sfera può percorrere in orizzontale. Da:
$$h_2 = \frac{1}{2}gt^2$$ si ottiene il tempo di volo
$$t_{volo} = \sqrt{\frac{2h_2}{g}}$$ da cui la gittata:
$$x = v t_{volo} = \sqrt{\frac{10}{7}gh_1 \frac{2h_2}{g}} \Longrightarrow x = \sqrt{\frac{20}{7}h_1h_2}$$

Si osservi che, nel caso di puro scivolamento (sfera puntiforme) si avrebbe: $x = 2 \sqrt{h_1h_2}$.

Effetto dell'attrito sul moto.
Le forme di dissipazione di energia per attrito sono due: l'attrito volvente durante il moto di rotolamento lungo la rampa e l'attrito viscoso (o "del mezzo") che si oppone al moto della sfera sia durante il rotolamento lungo la rampa sia durante la traiettoria parabolica. Come noto, l'attrito volvente è direttamente proporzionale alla forza normale alla superficie (nel nostro caso la componente della forza peso localmente normale alla rampa) ed inversamente proporzionale al raggio della sfera, pertanto il lavoro delle forze di attrito volvente durante il rotolamento sulla rampa è:
$$L_{vol} = \alpha \frac{mg}{R}$$
dove la costante di proporzionalità $\alpha$ tiene conto del coefficiente di attrito tra la rampa e la sfera, dell'inclinazione della superficie locale della rampa ed è proporzionale alla lunghezza AB della rampa stessa, per tener conto dello spostamento.
Per il calcolo del lavoro delle forze di attrito dovute alla viscosità dell'aria, è noto che la resistenza di attrito che una sfera incontra muovendosi in aria è:
$$D = \frac{1}{2} \rho v^2 C_D A$$
dove $\rho$ è la densità dell'aria, v la velocità relativa tra la sfera e l'aria, A l'area della sfera "vista" dall'aria ossia $A = \pi R^2$ e $C_D = 0,47$ è il coefficiente di resistenza della sfera.
La cosa che a noi interessa è che la forza di attrito con l'aria è direttamente proporzionale al quadrato sia della velocità della sfera sia del suo raggio; anche il lavoro fatto nel tratto AB della guida sarà quindi proporzionale al quadrato sia della velocità della sfera sia del suo raggio:
$$L_{vis} = \beta v^2 R^2$$dove anche in questo caso il coefficiente $\beta$ è proporzionale alla lunghezza della rampa.
Pertanto, tenendo conto di queste forme di dissipazione di energia meccanica, la conservazione dell'energia tra il punto di inizio della rampa ed il punto in cui la sfera lascia la rampa diventa:
$$mgh_1 - \alpha \frac{mg}{R} - \beta \bar{v}^2R^2 = \frac{1}{2}mv^2 + \frac{1}{5}mv^2 = \frac{7}{10} mv^2$$
dove $\bar{v}$ è una qualche velocità media compresa tra il valore nullo all'inizio della rampa ed il valore $v$ al termine della rampa, che sarà in qualche modo proporzionale a v, per cui:
$$ \bar{v}^2 = \gamma v^2$$
Sostituendo nell'equazione, dividendo per la massa della sferetta e risolvendo per $v$, si ha:
$$mgh_1 - \alpha \frac{mg}{R} - \gamma v^2 R^2 = \frac{7}{10} mv^2 \Longrightarrow \frac{7}{10} v^2 + \gamma v^2 \frac{R^2}{m} = gh_1 -\alpha \frac{g}{R}$$
da cui
$$v = \sqrt{\frac{gh_1 - \alpha \frac{g}{R}}{\frac{7}{10}+ \gamma \frac{R^2}{m}}}$$

Le costanti $\alpha$ e $\gamma$ e non sono facilmente determinabili, tuttavia sono certamente positive. Per questo, dall'espressione trovata della velocità v, si può dedurre che:

a parità di raggio, sfere aventi massa maggiore arrivino alla fine della rampa con velocità maggiore in quanto il denominatore della radice diminuisce;
a parità di massa, sfere con raggio maggiore arrivino al termine della rampa con velocità minore (il numeratore diminuisce ed il denominatore aumenta);
a parità di sfera (ossia usando la stessa sfera) se si aumenta l'attrito volvente con la rampa aumentando $\alpha$ la velocità al termine della rampa diminuisce.

Si può riscrivere l'espressione della velocità alla fine della rampa anche in termini della densità della sfera $\rho_s$:
$$v = \sqrt{\frac{gh_1 - \alpha \frac{g}{R}}{\frac{7}{10}+\frac{3 \gamma}{4 \pi} \frac{1}{\rho_s R}}}$$
Da questa riscrittura si evince che:

per sfere con lo stesso raggio, la sfera con maggior densità arriva in fondo alla rampa con velocità superiore (il denominatore diminuisce);
per sfere con la stessa densità, la sfera con raggio maggiore arriva in fondo alla rampa con velocità superiore (il numeratore aumenta ed il denominatore diminuisce).

Lo scopo dell'esperimento è di variare (per quanto possibile) diametro e massa della sfera (e quindi la sua densità) e il coefficiente di attrito tra la rampa e la sfera in modo da verificare se queste deduzioni teorica siano confermate dai fatti. Si osservi che, siccome non viene misurata la velocità al termine della rampa ma la gittata del moto parabolici che segue, è chiaro che la gittata sarà inferiore al valore teorico anche a causa di ulteriori perdite di energia dovute all'attrito con l'aria durante il moto parabolico. Tuttavia, sappiamo che queste perdite sono direttamente proporzionali al quadrato del raggio ed inversamente proporzionali alla massa della sferetta, per cui a parità di raggio sfere di massa maggiore hanno gittata maggiore, mentre a parità di massa sfere di raggio maggiore hanno gittata inferiore, in accordo con quanto osservato sopra.

Raccolta e analisi dei dati e calcolo del lavoro delle forze passive

Una volta misurati il diametro $D$ della sferetta (con il calibro), la massa $m$ della sferetta (con la bilancia elettronica), e le due altezze $h_1$ (altezza rispetto al tavolo da cui viene lasciata rotolare la sferetta) e $h_2$ (altezza del tavolo rispetto al pavimento), rimane da misurare esclusivamente la gittata $x$.
Nella misura delle altezze l'unico problema è che occorre tener conto delle posizioni del centro della sferetta, mentre la misura della gittata è più delicata in quanto bisogna misurare accuratamente la distanza tra il punto del pavimento sulla verticale dal bordo del tavolo (identificabile con il filo a piombo) e il punto in cui la sferetta impatta sul pavimento.

Per variare il coefficiente di attrito dinamico tra la sfera e la superficie della rampa conviene eseguire una serie di misure sulla rampa iniziale (di cartoncino) ed un'altra serie sulla rampa la cui superficie sia stata ricoperta con un panno da cucina che, essendo in qualche modo "spugnoso" non risponde elasticamente e dissipa molta più energia che nel caso di superficie non deformabile.

Nella sua versione più semplice l'esperimento può essere eseguito mantenendo costanti le altezze $h_1$ e $h_2$. Evidentemente ogni valore di gittata misurato sperimentalmente è inferiore a quello teorico a causa della dissipazione di una parte dell'energia potenziale inizialmente posseduta dalla sferetta. Se con $h$ indichiamo l'altezza ideale che, in assenza di attriti, causerebbe la gittata misurata $x$, invertendo la formula della gittata teorica si ha:
$$x = \sqrt{\frac{20}{7}h_2h} \Longrightarrow h = \frac{7}{20} \frac{x^2}{h_2}$$

L'energia persa sotto forma di lavoro totale di tutte le forze non conservative è la differenza tra l'energia potenziale iniziale posseduta dalla sferetta e quella (inferiore) che sarebbe stata necessaria per raggiungere la gittata reale in assenza di dissipazioni:
$$L_a = mg \left(h_1 - h \right) = mg \left( h_1 - \frac{7}{20} \frac{x^2}{h_2} \right)$$
Ovviamente il lavoro delle forze di attrito è proporzionale al peso della sferetta. Per quantificare le perdite relative, si può calcolare la perdita percentuale di energia rispetto all'energia meccanica inizialmente posseduta dalla sfera, i.e.
$$ L_{a\%} = \frac{L_a}{mgh_1} \cdot 100 = \left( 1 - \frac{7}{20} \frac{x^2}{h_1h_2}\right) \cdot 100$$
Nella tabella seguente vengono riportati i dati ottenuti da un gruppo di studenti durante l'esperienza in classe (il valore della gittata è la media aritmetica su 10 prove): i valori della altezze portano ad un valore di gittata teorica (in assenza di attriti) pari a $x = 0,754 \cdot 10^{-2}\ m$. Oltre ai dati grezzi, in tabella vengono riportati anche la densità della sfera $\rho_s$, il lavoro delle forze di attrito ed il suo peso percentuale rispetto all'energia inizialmente posseduta dalla sfera:

tabella 1: valori sperimentali misurati in sei diversi esperimenti e valori calcolati del lavoro delle forze dissipative.

Considerazioni al variare delle caratteristiche della sfera e della rampa. La parte più interessante dell'esperimento consiste nel verificare come cambia il lavoro delle forze di attrito al cambiare del raggio o della massa della sfera e della superficie della rampa. Osservando i dati riportati in tabella e le perdite percentuali di energia per attrito si può concludere che:

la superficie di cartoncino (rigida) offre molto meno attrito rispetto alla superficie spugnosa in quanto è difficilmente deformabile e, per questo, non assorbe molta energia (si confrontino i casi 1 e 4 in cui è stata utilizzata una sfera grande in acciaio, i casi 2 e 5 in cui la sfera in acciaio era più piccola, ed i casi 3 e 6 in cui si è usata una sfera grande in alluminio);
la sfera che incontra il minor attrito, a parità di superficie della rampa, è quella con maggior massa e maggior raggio poiché, come osservato in precedenza, un raggio ed una massa elevati riducono sia l'attrito di rotolamento che quello viscoso con l'aria;
a parità di raggio (esperimenti 1 e 3, oppure 4 e 6), la minor perdita di energia si ha per la sfera con maggior massa in quanto al crescere della massa diminuisce l'effetto dell'attrito viscoso con l'aria;
a parità di densità (le densità delle 2 sfere in acciaio negli esperimenti 1 e 2 e 4 e 5 differiscono per circa il 3.4%) la sfera con maggior raggio subisce minori perdite per attrito.

Minimizzazione delle fonti di errore.
Le misure delle altezze e delle caratteristiche delle sferette non dovrebbero dare troppi problemi. Al contrario, si verifica che le misure della gittata, a parità di tutti gli altri parametri, può dare origine ad una certa dispersione dei dati. Questo potrebbe essere dovuto al fatto che l'altezza iniziale non è sempre la stessa o al fatto che viene involontariamente impressa una velocità non nulla alla sferetta nel punto A. E' utile far ragionare gli studenti su questo problema e discutere con loro di come si potrebbe minimizzare questa incertezza. Un altro problema è il raccordo della fine della rampa con il tavolo, che non deve presentare "salti".

Note e storia

Nota: sono previste due ore per la realizzazione dell'esperienza unicamente perché la realizzazione della rampa richiede del tempo così come la copertura della sua superficie con un panno da cucina in modo che aderisca perfettamente alla rampa (per questo è meglio utlizzare un nastro bi-adesivo). Al contrario. l'esperimento in sè è piuttosto veloce in quanto le grandezze da misurare sono poche e semplici (una massa e quattro lunghezze). Per ridurre i tempi di realizzazione ad una sola ora, si può assegnare la realizzazione della rampa come compito per casa, in preparazione all'esperimento.

Bibliografia

Autori

Zuccher Simone

Energia dissipata nel moto di rotolamento lungo una rampa